In my opinion, you should try to solve the problem on your own at first and try to understand why there's a need for the disjoint set data structure. Essentially, the cases where matrix cell values are equal will become hard to assign a rank. There's a good explanation with visualization of it here - votrubac's answer: click me.
Essentially the case where disjoint-set is needed is shown below (credits to the author of this image - votrubac):
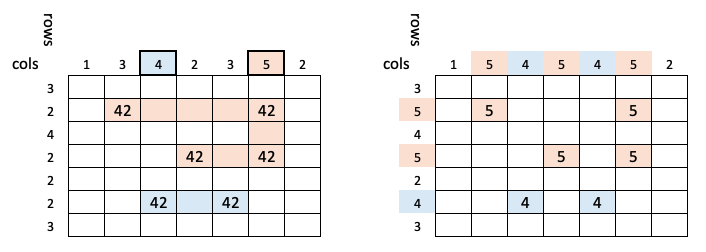
This helps a lot to understand the need for a disjoint-set.
DSA Pre-requisites
First of all, you need to know how a basic Disjoint-Set data structure (with Union-Find algorithm) works. You can learn it at GFG Union-Find
For shortening the runtime complexity, Union-Find is implemented with 2 optimizations: a. union by rank (which reduces union & find runtimes to O(log2(n)), and b. path compression (which reduces union & find time runtimes further to an amortized constant. You can learn it at GFG Union-Find by Rank
Logic
The logic is as below:
- Store all the cells which have equal value together.
- Traverse the cells from lowest to highest value (this is why a TreeMap is used to store)
- Store max of each row and each col in an array (maxRowColValues) to compare and find the next max rank of a cell
- For each group of cells with equal values (like for 42 in the image above):
- Create a disjoint set for each row and each col
- Unite x & y coordinates of each cell
- Form new groups of the united cells via their root cell (coordinatesByRoot)
- Assign rank + 1 to each group based on the max(rank) of the rows and cols they belong to
- Do not forget to increase the max of each row and each col (maxRowColValues)
Code (Java)
Note: A cell is referred to as coordinate below. I have tried to make the code as much understandable and maintainable as possible, yet all kinds of suggestions are welcome to make it even more understandable
public int[][] matrixRankTransform(int[][] matrix) {
int rows = matrix.length, cols = matrix[0].length;
int[][] rankMatrix = new int[rows][cols];
// Create a TreeMap with the matrix cell values as keys since it stores keys in ASCENDING order
TreeMap<Integer, ArrayList<Coordinate>> coordinatesByVal = new TreeMap<Integer, ArrayList<Coordinate>>();
for (int r = 0; r < rows; r++) {
for (int c = 0; c < cols; c++) {
int val = matrix[r][c];
if (coordinatesByVal.get(val) == null) {
ArrayList<Coordinate> coordinates = new ArrayList<Coordinate>();
coordinates.add(new Coordinate(r, c));
coordinatesByVal.put(val, coordinates);
} else {
coordinatesByVal.get(val).add(new Coordinate(r, c));
}
}
}
// Create an array to store max for each row and col; cols start after rows
int[] maxRowColValues = new int[rows + cols];
// Assign ranks to coordinates of each val starting from lowest val
for (int val: coordinatesByVal.keySet()) {
ArrayList<Coordinate> coordinatesWithSameVal = coordinatesByVal.get(val);
// Create a copy of maxRowColValues to make edits here; O(rows + cols)
int[] maxRowColValuesClone = new int[rows + cols];
for (int i = 0; i < maxRowColValues.length; i++) {
maxRowColValuesClone[i] = maxRowColValues[i];
}
DisjointSet disjointSet = new DisjointSet(rows + cols); // each row and each col is now a subset of itself; O(rows + cols)
for (Coordinate coordinate: coordinatesWithSameVal) {
disjointSet.uniteSubsets(coordinate.x, coordinate.y + rows); // rows is added because 0 to rows-1 is for x-coordinates
// Total time over complete matrix: O([rows + cols] log2([rows + cols]))
}
// Group coordinates with the same root
HashMap<Node, ArrayList<Coordinate>> coordinatesByRoot = new HashMap<Node, ArrayList<Coordinate>>();
for (Coordinate coordinate: coordinatesWithSameVal) {
Node root = disjointSet.findRoot(coordinate.x); // y val is already united with x, so no need to find it
if (coordinatesByRoot.get(root) == null) {
ArrayList<Coordinate> nodes = new ArrayList<Coordinate>();
nodes.add(coordinate);
coordinatesByRoot.put(root, nodes);
} else {
coordinatesByRoot.get(root).add(coordinate);
}
}
// Get maxRowColVal of each group and assign it to their rankMatrix cell
for (Node root: coordinatesByRoot.keySet()) {
ArrayList<Coordinate> groupCoordinates = coordinatesByRoot.get(root);
// Get maxRowColVal of each group
int maxRankOfGroup = 0;
for (Coordinate coordinate: groupCoordinates) {
int x = coordinate.x, y = coordinate.y;
maxRankOfGroup = Math.max(maxRankOfGroup, Math.max(maxRowColValues[x], maxRowColValues[y + rows]));
}
// Assign new rank to each coordinate and then to all row-col values
for (Coordinate coordinate: groupCoordinates) {
System.out.println("Assigning rank " + (maxRankOfGroup + 1) + " to [" + coordinate.x + ", " + coordinate.y + "]");
rankMatrix[coordinate.x][coordinate.y] = maxRankOfGroup + 1;
maxRowColValues[coordinate.x] = maxRankOfGroup + 1;
maxRowColValues[coordinate.y + rows] = maxRankOfGroup + 1;
}
}
}
return rankMatrix;
}
class Coordinate {
int x, y;
Coordinate(int x, int y) {
this.x = x;
this.y = y;
}
}
class Node {
int parent;
int rank;
Node(int parent, int rank) {
this.parent = parent;
this.rank = rank;
}
}
class DisjointSet {
Node[] subsets;
DisjointSet(int numOfSubsetsAtStart) {
this.subsets = new Node[numOfSubsetsAtStart];
for (int i = 0; i < numOfSubsetsAtStart; i++) {
subsets[i] = new Node(i, 1);
}
}
// Find root parent of a number; this is essentially the "FIND" function of Union-Find
Node findRoot(int num) {
if (subsets[num].parent == num) {
return subsets[num];
} else {
Node root = findRoot(subsets[num].parent);
subsets[num].parent = root.parent; // This is path compression
return root;
}
}
// This is essentially "UNION BY RANK"; hence unions take log2(number of subsets)
void uniteSubsets(int val1, int val2) {
Node root1 = findRoot(val1);
Node root2 = findRoot(val2);
if (root1.rank < root2.rank) {
// Since root2 has higher rank, root1 should be added as a child, otherwise root1's rank will be even higher
root1.parent = root2.parent; // BTW root2.parent will always be its index in subsets array
// No need to increase rank of root2, since its anyways higher
} else if (root2.rank > root1.rank) {
root2.parent = root1.parent; // No need to increase rank of root1, since its anyways higher
} else {
root1.parent = root2.parent;
root2.rank++; // Both have same rank, hence the rank of the new parent needs to be increased
}
}
}
Happy coding!

